|
Mach-Ultimate the ultimate Dsing-Model |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
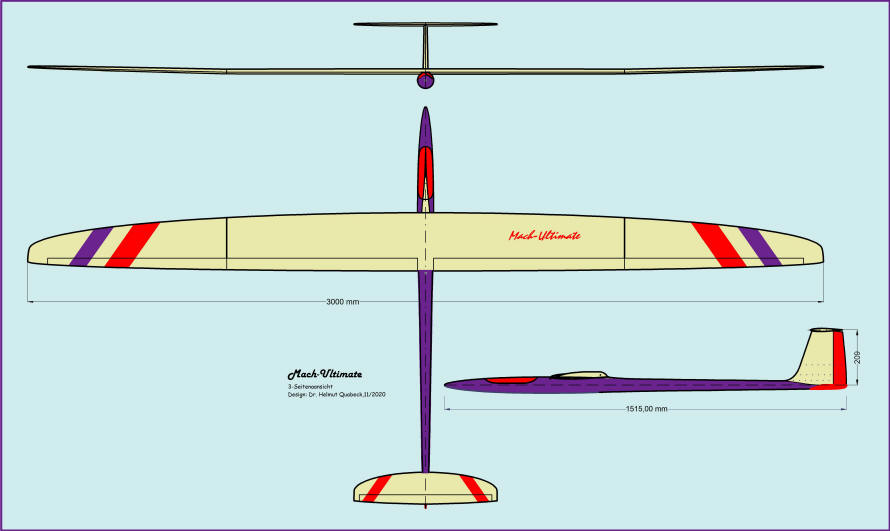
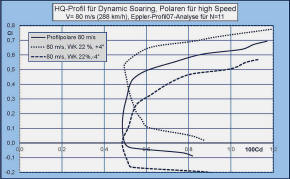
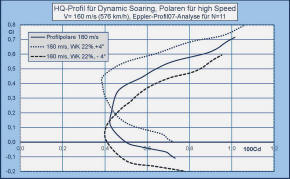
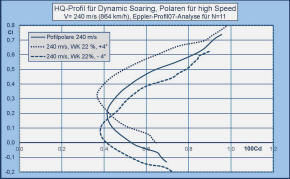
Ein paar theoretische Aspekte zum Modell Die Erfahrungen mit dem "Orbiter" -Modell beim DS-Fliegen am Parker Mountain in Kalifornien haben mich dazu veranlasst, eine verbesserte DS-Version, eine "Mach-Ultimate", zu entwickeln. Bruce Tebo erzielte zwar vor einem Jahr bei mäßigen Windbedingungen mit dem Orbiter -Urmodell ca. 660 km/h, aber eine weitere Steigerung der Geschwindigkeit war ihm leider nicht möglich, weil beim Durchfliegen der Scherwinde an der Hangkante der Rumpf anfing zu schwingen. Umso mehr wird beim neuen Modell beachtet werden, dass die Biegesteifigkeit des Rumpfes den hohen Biegemomenten im Schnellflug standhält. Die wesentlichen Veränderungen sind: 1. ein Profil mit etwas geringerer Dicke und leicht erhöhter Wölbung, das im Schnellflug ohne Wölbung einen geringsten Widerstandsbeiwert von cd = 0,004 bei einem Auftriebsbeiwert von cl = 0,2 liefert, 2. eine erhöhte Streckung der Tragfläche und eine geringere durchschnittliche Flächentiefe, so dass der Flächeninhalt etwa dem des "Orbiters" entspricht, 3. Übernahme des "Orbiter" -Rumpfes mit einer leichten Erhöhung (Vergrößerung) des Seitenleitwerks, die erforderlich ist, um die streckungsbedingten größeren Trägheitsmomente der Tragflügelhälften im Langsamflug zu kompensieren. Wie im Weiteren noch erläutert wird, resultieren für das gewählte Profil beim "Dsing" mit cl = 0,2 komfortable lokale Kreisradien bei unterschiedlichen Flächengewichten von 5 bis 15 kg/m2. Was aber insbesondere daraus folgt, sind sehr geringe induzierte Widerstandsbeiwerte, die kleiner sind als die Werte von Höhenleitwerk, Seitenleitwerk und Rumpf und weniger als ein Zehntel des Widerstandsbeiwertes der Tragfläche ausmachen. Eine weitere Erhöhung der Streckung würde sich beim schnellen DS-Fliegen nicht bemerkbar machen. Wichtiger: Die Flächenform wurde wiederum so gewählt, dass auch an den Außenteilen der Fläche noch Profiltiefen mit guten Re-Zahlen für die Luftströmung erreicht werden, so dass der Flügel insgesamt einen geringeren durchschnittlichen Widerstand liefert als der des Orbiters. Die nachstehenden Grafiken zeigen die Auftriebs-Widerstandspolaren des Tragflächenprofils für Fluggeschwindigkeiten von V = 80 m/s, 160 m/s und 240 m/s, was in etwa den üblichen niedrigen und hohen DS-Geschwindigkeiten entspricht. Die Re-Zahlen in den Grafiken entsprechen den durchschnittlichen Flächentiefen des Modells und den angeführten Geschwindigkeiten. In den Polarengrafiken sind nicht nur die Polaren für das ungewölbte Profil, sondern auch jeweils solche für +/- 4° Wölbklappenausschlag bei einer Klappentiefe von 22 % der Profieltiefe eingetragen. Die damit zu erreichenden Auftriebsumfänge sind insbesondere z.B für das Slope-Soaring von großem Interesse. Was dabei auffällt, ist, dass beim Wölben im hohen Geschwindigkeitsbereich die Profilwiderstände theoretisch nahezu konstant bleiben. Beim DS-Fliegen wird man mittels Snap-Flap besonders von negativen Klappenausschlägen in der Sturzflugphase profitieren können. Positive Ausschläge könnten in der DS-Schleife leicht zur Erhöhung der Auftriebsbeiwerte mit unerwünschtem Anstieg des induzierten Widerstandes führen. In der Folge wird noch aerodynamisch erläutert werden, wie mit einem Auaftriebsbeiwert von cl = 0,2, bei dem das Profil etwa seinen geringsten Widerstand hat, die DS-Schleifen am besten zu fliegen sind. Dabei sind neben dem Auftriebsbeiwert das Flächengewicht des Modells, die Bahnneigung und die Schräglage um die Längsachse die ausschlaggebenden Parameter für den lokalen Radius der DS-Flugbahn. Dazu bedarf es einiger aerodynamischer und flugmechanischer Ausführungen, die nachfolgend in einer Formelsammlung zusammengefasst sind: Zunächst seien die Bezeichnungen der maßgeblichen Parameter und Charakteristika zusammengestellt: Trägheitskraft: K [N = Newton] Auftriebskraft L [N], (L = Lift) Widerstandskraft: D [N], (D = Drag) Zentrifugalkraft: ZR [N] Gewichtskraft: G = m x g [N] Masse: m [kg] Erdbeschleunigung: g [m/s2] (= 9,81) Geschwindigkeit: V [m/s] Luftdichte: r (rho) [kg/m3) (= 1,25 bei NN) lokale Bahnneigung: j (phi) Schräglagewinkel: Q (Theta) Auftriebsbeiwerte: cl (Profil), cL (Modell) Widerstandsbeiwerte: cd (Profil), cD (Modell) Profiltiefe: c [m] , ĉ (durchschnittlich) Tragfläche: A [m2] HLW-Fläche: AH [m2] SLW-Fläche: AS [m2] Der Auftriebsbeiwert der Tragfläche ist aufgrund von Wirbelbildungen geringer als der des Profils und hängt von Form und Streckung der Fläche ab. Der Effizienzfaktor des Auftriebsbeiwertes aA lässt sich berechnen und ist für die Mach-Ultimate = 0,9 (= 90 %). ĉL = aA x ĉl Damit sind die Voraussetzungen zum Verständnis der nachstehenden aerodynamischen Ausführungen zum Dynamic Soaring gegeben:
Bei der Berechnung der lokalen Kreisradien ist zu beachten, dass sich der Neigungswinkel des Modells auf der DS-Schleife stetig ändert. Am oberen und am unteren Ende der Schleife ist der Neigungswinkel 0°, an den Seiten, wo das Modell die steilste Flugbahn - nach unten wie nach oben - einnimmt, ist in den Beispielen der maximale Neigungswinkel mit 30° angenommen worden. Mit der "Mach-Ultimate" sollten die Kreisradien mindestens so groß, wie in den Tabellen angegeben, geflogen werden, um den induzierten Widerstand, der vom Quadrat des Auftriebsbeiwertes abhängt, zu miminieren. Bisher wurde noch nicht berücksichtig, wie sich das Modell beim Durchgang durch die Scherwinde an der Hangkante im oberen Teil der DS-Schleife zu verhalten hat, um die dort entstehenden zusätzlichen Auftriebskräfte - den eigentlichen Motor des DS-Fliegens - für eine Beschleunigung der Geschwindigkeit zu nutzen. Je nach Hang und Wind ist der Scherwindbereich in dem das Modell zusätzlichen Auftrieb erfährt unterschiedlich hoch. Läßt man das Modell im Hangaufwind zu hoch steigen, wird es erfahrungsgemäß wegen seiner Massenträgheit an Fahrt verlieren und der Widerstand kann sich erhöhen. Es sind die Erfahrung und das Geschick des Piloten, den Hangaufwind so zu durchfliegen, dass das Modell dabei größtmögliche Beschleunigung erfährt. Dies ist wiederum nur möglich, wenn der Profilwiderstand des Modells minimal ist, was beim "Mach-Ultimate" etwa bei cl = 0,2 der Fall ist. Verschiedene Videos von Bruce Tebo und Spencer Licenby, den Top-Piloten der Szene, zeigen, dass sie ihre DS-Schleifen meist in Form einer mit der Längsachse nach oben weisenden Linse mit etwa 30° Neigung fliegen. Auch hier gilt, die lokalen Kreisradien so zu wählen, dass der Auftriebsbeiwert im Falle der "Mach-Ultimate"-Fläche <= 0,2 bleibt. Natürlich kommt es auf die lokalen Gegebenheiten und das Vermögen des Piloten an! Manchmal braucht es bis zu 45° Bahnneigung, z.B. hinter einer Baumgruppe, manchmal reichen schon 20°. Noch ein Kommentar zur Berechnung der Umfangsgeschwindigkeit: Da es sich beim Dynamic Soaring nicht um eine stationäre, sondern eine dynamische Bewegung des Modells handelt, ändert sich der Widerstand fortlaufend mit der Bewegung auf der Umlaufbahn. Kennt man z. B. die Ausgangsgeschwindigkeit Vo mit s=0 im Zenit der Bahn, kann man unter Berücksichtigung des Widerstandsbeiwerts, der sich mittels lokaler Re-Zahl und lokalem Auftriebsbeiwert näherungsweise für eine kurze Wegstrecke s ergibt, die Geschwindigkeit am Ende dieses Weges berechnen. Geht man auf diese Weise weiterhin iterativ vor, läßt sich die Geschwindigkeit für einen beliebigen Punkt auf der Schleife bestimmen. Aber das ist eher eine Aufgabe für numerische Mathematiker. (Ähnliche Aufgaben wurden von mir z.B. für den Windenhchstart eines Segelmodells, für die Optimierung desr Flugbahn ibeim F3B-Speedflug, für den Kreisflug und anderes mehr in meinem Theoriebuch " Design, Leistung und Dynamik von Segelflugmodellen" berechnet.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Hier wird noch weiter über das neue Modell "Mach-Ultimate", für schnelles Hangfliegen und Dynamic Soaring berichtet werden! |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Neu
Update 25
*
HQ-Profile
Update 2023
*
Neuer 6 M-Segler
*
8 M-Segler von RCFA
*
Leistungs-potential
*
2021-Dsing
*
Reportagen:
Konstruktionen:
*